慣性モーメント(イナーシャ)Jの計算式･公式 一覧

最終更新日時：2020年6月25日

基本の公式

慣性モーメントは、回転体の中心を回る「回転体の質量Ｍ [kg]と回転体の半径Ｒ[m]の２乗との積」の式が基本となります。
また回転中心がずれている、物体の形状が円筒ではない、直線運動をするといった場合でも、どの位置で何が回転しているのかがわかれば慣性モーメントを計算することができます。

慣性モーメント＝質量×半径²（J=M･R²）

慣性モーメント計算式

中空円筒の慣性モーメント計算式

D : 円筒の外径[m]
d : 円筒の内径[m]
M : 円筒の質量[kg]

J=	1	M(D2 + d2) [kg･m2 ]
	8

【計算例】

製品：サーボリジッドカップリング「SRG-050DS」
質量M：0.45［kg］（最大穴径時）
外径D：48×10^-3［m］
穴径d：22×10^-3［m］（最大穴径）
※製品にはテーパ面などがありますが、単純な中空円筒とみなして計算します。

J=	1	×0.45｛(48×10-3)2+(22×10-3)2}
	8

　=156×10^-6
　=0.16×10^-3

※カタログの慣性モーメントと同じ値となりました。

製品の詳細を見る

回転中心がずれた場合の円筒の慣性モーメント計算式

r : 回転半径[m]
D:円筒の直径[m] M : 円筒の質量[kg]
J_A : 円筒の中心A回りの慣性モーメント[kg･m ² ]

J=JA + M･r2

=	1	M･D2 + M･r2
	8

=	1	M(D2 + 8r2)[kg･m2]
	8

回転する棒の慣性モーメント計算式

L : 棒の長さ[m]
M : 棒の質量[kg]

J=	1	M･L2 [kg･m2 ]
	3

回転中心がずれた場合の棒の慣性モーメント計算式

L₁, L₂ : 回転中心からの距離 [m]
M : 棒の質量[kg]

J=	1	M(L12 + L1L2 + L22) [kg･m2 ]
	3

巻き上げ機構の慣性モーメント計算式

J_A : ドラムの慣性モーメント[kg･m²]
D : ドラムの直径[m]
M : 負荷の質量[kg]
M_A : ドラムの質量[kg]

J=JA +	1	M･D2
	4

=	1	MA･D2 +	1	M･D2
	8		4

=	1	D2(MA+2M) [kg･m2 ]
	8

カウンターバランスがついているときの慣性モーメント計算式

J_A : ドラムの慣性モーメント[kg･m²]
D: ドラムの直径[m]
M ₁,M₂ : 負荷の質量[kg]
M_A : ドラムの質量[kg]

J=JA +	1	(M1+M2) D2
	4

=	1	MA･D2 +	1	(M1+M2)D2
	8		4

=	1	D2(MA+2M1+2M2) [kg･m2 ]
	8

直方体の慣性モーメント計算式

a, b : 辺の長さ[m]
M : 直方体の質量[kg]

J=	1	M(a2 + b2)[kg･m2 ]
	12

送りねじによる直線運動をする物体の慣性モーメント計算式

J_A : 送りねじの慣性モーメント[kg･m²]
P : 送りねじのリード[m]
M : 負荷の質量[kg]

J=JA +	M･P2	[kg･m2 ]
	4π2

ラックピニオンで動かすときの慣性モーメント計算式

J_A : ピニオンの慣性モーメント[kg･m²]
D : ピニオンの直径[m]
M : ラックと負荷の質量[kg]

J=JA +	1	M･D2 [kg･m2 ]
	4

ベルトコンベアの慣性モーメント計算式

J_A : ローラの慣性モーメント[kg･m²]
D : ローラの直径[m](左右同径とする)
M : 負荷の質量[kg]
M_A : ローラの質量[kg]

J=JA +	1	M･D2
	4

=	1	(MA+MA)D2 +	1	M･D2
	8		4

=	1	D2(MA+M) [kg･m2 ]
	4

ワークがローラに挟み込まれた状態の慣性モーメント計算式

J_A : ローラAの慣性モーメント[kg･m²]
J_B : ローラBの慣性モーメント[kg･m²]
D_A : ローラAの直径[m]
D_B : ローラBの直径[m]
M: ワークの等価質量[kg]
M_A : ローラAの質量[kg]
M_B : ローラBの質量[kg]

J=JA+ (	DA	)2JB +	1	M･DA2
	DB		4

=	1	MA･DA2+	DA2	･	1	･MB･DB2+	1	M･DA2
	8		DB2		8		4

=	1	DA2(MA+MB+2M) [kg･m2 ]
	8

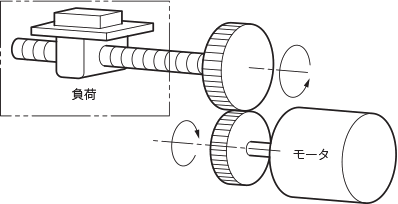
モータ軸換算慣性モーメント計算式

Z₁: モータ側ギヤの歯数
Z₂ : 負荷側ギヤの歯数
R : 減速比 Z₂/Z₁
J_A : 負荷の慣性モーメント[kg･m²]
J₁ : モータ側ギヤの慣性モーメント[kg･m²]
J₂ : 負荷側ギヤの慣性モーメント[kg･m²]

J=J1 +(JA + J2)･(	1	)2	[kg･m2 ]
	R

慣性モーメント(イナーシャ)とは？

慣性モーメントとは物体の回されやすさ、されにくさの度合いです。
※英語ではmoment of inertiaとなるので、イナーシャということもあります。
※計算式では従来「I」と表示していましたが、電流と間違えるので現在では「J」で表示しています。

たとえば、ピンポン玉とピンポン玉と同じ大きさの鉄球をある速度まで転がすことを考えます。
ピンポン玉は軽い力で転がり出します、しかし鉄球を動かすのには、ピンポン玉より力が必要です。
逆にある速度で転がっているピンポン玉と鉄球とでは自然に停止するまで、鉄球の方がはるかに時間と距離が必要です。
これを強引に停止させようとすると、鉄球の方が力が必要になります。
このように、物体をある速度まで動かすときの動かし易さ、物体をある速度から停止させようとしたときにどのくらい力が残っているかを慣性と呼び表します。



つまり慣性モーメントが大きければ回転や停止がしにくいので、たとえば正逆転を繰り返す機械（ご使用いただく三木プーリ製品も含めて）の慣性モーメントは小さい方が制御しやすい機械であるといえます。
さらに制御しやすければ振動を抑えて機械の精度を上げることができるので、高精度の製品が得られることになります。

慣性モーメントの必要性

なぜ慣性モーメントを計算する必要があるのでしょうか。
先ほど慣性モーメント(イナーシャ)とは？でも高精度の製品が得られると述べましたが、それは次に示す慣性モーメントとトルクの関係式があるからです。
回転トルクT[N･m]＝慣性モーメントJ[kg･m²] × 角加速度α[rad/sec²]

角加速度とは物体が回転するときの単位時間当たりの角速度の変化で、角速度を時間微分したもの。単位はラジアン毎秒毎秒です。
静止している物体をある加速度（あるいは角加速度）で回転させるために必要なトルク、もしくは回転している物体を止めるためのトルクを求めるには、このように慣性モーメントの値が必要となるのです。

よって慣性モーメントを求めるだけではなく、慣性モーメントの値からさまざまな関係式を用いて最適な機械系を得ることが重要となります。

国際単位系と重量単位系

現在では慣性モーメントは国際単位系の　J＝M･R²［kg･m²］　を使用しています。
また従来の重量単位系では、　I=W･R²／g [kgf･m･s²] 　としていました。（W：重量、g：重力加速度）
さらに従来の重量単位系において、　GD²＝W･D²［kgf･m²］　もありました。（D：回転体の直径）
このGD²は「はずみ車効果」ともよばれており、特にモータなどの計算に使われていました。

はずみ車はフライホイールともよばれています。
たとえば停電などで急に回転速度が落ちると、機械に衝撃が伝わり破損する恐れがあります。
これは急停車する電車の中にいる人達にかかる負荷と同じような考え方です。
そこでゆっくりと回転速度をおとすために、慣性モーメントの大きい回転体を取り付けます。これがフライホイールです。

この他にもエンジンの出力回転には、ピストン運動による回転ムラが発生しています。
フライホイールによって、この回転ムラを減らして安定させることができるのです。

その他の技術資料